ほしい書籍や電化製品があったならば、インターネットでマウスを数クリックしただけで数日後、早ければ翌日には希望の商品が届きます。

今の時代ならば、決してめずらしいことではありません。たとえ無人島であっても、ネットショップから荷物さえ届くなら問題なく生きていけるとさえ言われるほどです。

ネット上での買い物を可能にしているのが、暗号技術です。購入情報や住所、クレジットカードの番号などが、悪意ある第三者の手にわたったとしても、暗号化されているため解読は「ほとんど不可能」といえるほど困難、と考えられています。

しかし、これが意外にも「多分大丈夫だろう」というレベルであり、簡単に解読されてしまうかもしれない可能性をいまだに排除できていないというのはご存知でしょうか？

スポンサーリンク

原始的な「シーザー暗号」

意外に簡単に解読できそうといっても、強固であることに変わりはありません。まずは、現在の暗号がどれほど安全なものなのかを知るため、原始的な暗号に触れましょう。

ローマ帝国の帝王、カエサルが使用したと言われている「シーザー暗号」というものがあります。現在使われている暗号においても重要な要素「規則」と「鍵」がそなわっています。

「EBIIL」

これは、暗号文なので意味はさっぱりわからないはずです。しかし、「アルファベット順に3文字ずらして読んで」という取り決めを、あらかじめ聞いていたとすれば、解読ができるでしょう。

「アルファベット順にずらす」が規則であり、「3文字」が鍵となります。しかしこの暗号の弱点はとても多く、当時でさえ軍事目的では使われませんでした。

長い文章の暗号文となれば、それぞれの文字の使用率を割り出せば「規則」も「鍵」も解くことが可能なのです。

解き方をだれでも知っている？

現代の暗号は、不特定多数が取引を行えるようになっているため、その仕組みを調べようと思えばだれでも可能です。むしろ知らずとも暗号の利用が可能で、それらはコンピュータが代行してくれます。

シーザー暗号でいえば「規則」にあたる部分が広く公開されており、言ってみれば暗号の半分は解けたも同然です。それどころか、「鍵」の部分ですら公開されています。

実は、この「公開する鍵」の存在が昔の暗号と大きくちがう部分であり、軍事目的のみならず広く使われる理由にもなっています。

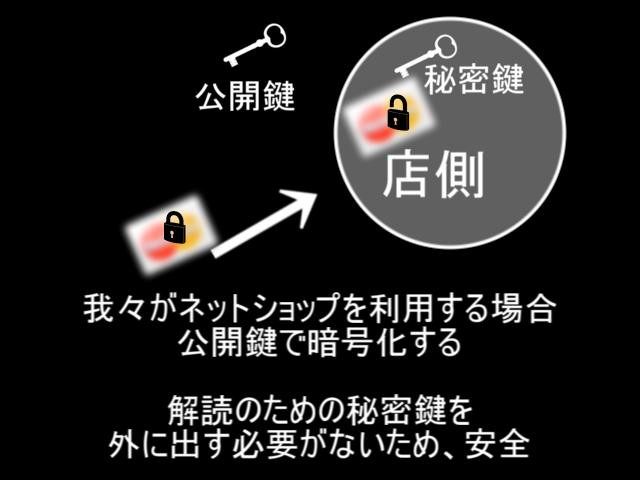
この、新しい暗号を使用する者は、それぞれ「公開鍵」「秘密鍵」の、二種類の鍵を持っています。「公開鍵」で暗号化された暗号は、もう一つの「秘密鍵」でのみ解読できる、という関係なのです。

スポンサーリンク

あなたがネットで取引をおこなう場合、相手の「公開鍵」であなたの個人情報を暗号化し、送信します。この暗号は「公開鍵」で解読することはできません。取引相手だけが持っている「秘密鍵」を使った場合のみ、解読が可能です。

このような、不思議な仕組みを実現しているのが「一方向性関数」です。

一方向性関数とは？

59×43＝？

上記の問題がいくつになるか、すぐに分かるでしょうか。答えは「2537」です。暗算に慣れていない方でも、紙とペンがあれば、そう難しくはないでしょう。では、下記はどうでしょうか？

？×？＝2537

答えはいくつかありますが、実はさきほどの問題を逆にしただけなので、答えは上に記されているとおり「59×43」です。これを自力で求めようとした場合は、かなり難しいでしょう。

「59×43＝2537」は簡単ですが、2537という答えを分解し、59×43に辿り着くのはかなり面倒です。このような、逆方向への計算が非常に難しい問題を「一方向性関数」と呼びます。

2桁×2桁ならばともかく、100桁×100桁と桁数が増えていけば、コンピュータにすら簡単に解くことができません。このような仕組みが実際の暗号に利用されています。

現在使われている暗号の場合、スーパーコンピュータで計算しても、数千～万年かかると言われています。これが、現代の暗号が事実上安全であることを保証しています。

解読は実は簡単かもしれない？

一方向性関数は、逆方向への計算がとても困難です。しかし、これが数学的に証明されているわけではありません。実は、簡単に計算できてしまうような計算方法が、探しているうちに見つかるかもしれないのです。

有史以来、人間はさまざまな計算方法を考えだし、それまではむずかしかった計算を、いとも簡単に回答をみちびきだせるようになりました。

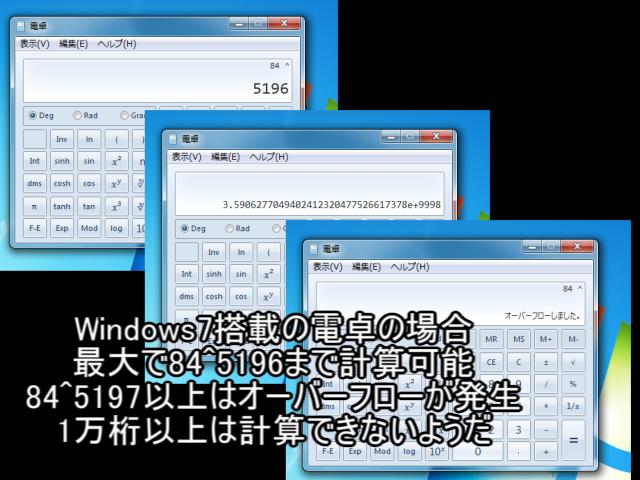
たとえば、84を483625回掛ける、という途方もなく長い計算をおこない、これが何桁になるのかを、電卓を使って調べてみましょう。

一般的な電卓の場合「84××」に続けて＝を483625回押す、という不毛なことを実行すれば計算可能ですが、実際には多くとも数十回ほど押した時点でエラーになるでしょう。

より多くの桁が計算できる関数電卓があったとしても、桁数が多すぎればエラーが出ます。しかし、常用対数という不思議な計算式を使えば、およそ93万桁になることがすぐにわかってしまうのです。

このように、本来ならば計算不可能に見えるような問題であっても、計算方法ひとつで簡単に解けてしまった例はいくつもあるのです。暗号に使われている計算方法であっても、革命的な計算方法が判明してしまえば、暗号は安全でなくなってしまいます。

安全を決めるP≠NP予想とは

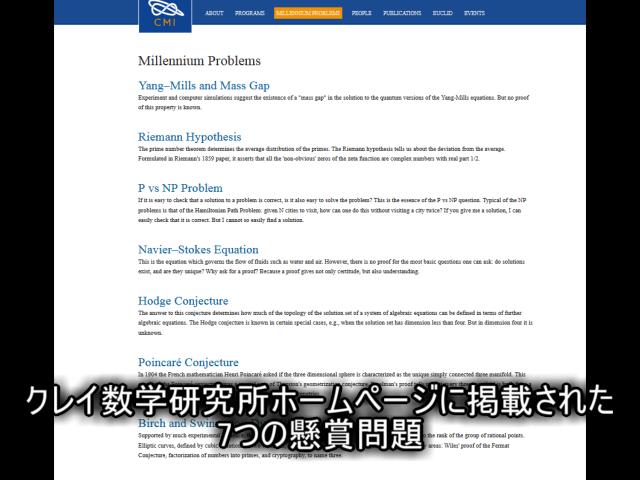
100万ドルの懸賞金がかけられた超難問のひとつ「P≠NP予想」が、実は暗号と密接な繋がりがあります。

先ほどの問題「59×43」は簡単に計算できますが、その逆方向である「2537＝？」については、長い時間をかけて計算するしかありません。

逆方向への計算に、効率のよい計算方法は絶対にない、とするのがP≠NPであり、多くの数学者がその方法を探しているにもかかわらず未だに見つかっていない以上、多分ないだろうと「予想」しているために「P≠NP予想」と呼ばれています。

もし、この予想が成立した場合は、今の暗号は絶対安全だと言えます。しかし予想が成立しなかった場合は、効率のよい計算方法があるかもしれないのです。

私たちが絶対に安全だと思っているインターネット取引も、もしかしたらいつか崩壊するときが来るかもしれないのです。それが数分後かもしれませんし、絶対に来ないかもしれません。

Byヒビタカ

スポンサーリンク